電気通信主任技術者(線路)の専門科目である「通信線路」の問5に頻出されている牽引張力の計算問題について解説していきます。
近年で毎回1問は必ず出題されていますので、この計算問題を確実に解けるようにして3点を確保しましょう!
公式とパターンを覚えるだけで解けますので、参考にしてみて下さい。
牽引張力と張力の公式
さっそくですが、「牽引張力の公式」と「弛度と張力の公式」を覚えましょう!
・曲線区間 T=(To+μgLW)K
・屈曲部直後 T=ToK
To:敷設区間直前の張力
μ:摩擦係数
g :重量加速度
L :敷設対象区間の長さ
W :単位長当たりのケーブル重量
K=e(μθ)乗:張力増加率
※上記の公式は、令和1年第2回の問5(1)にも出題されています。
張力を求める式に変化すると、
・張力 T=WS2乗/8D・・・②
D :弛度
W:単位長さ当たりのケーブル重量
S:スパン長
T:張力
2年分(年2回の4試験分)の過去問利用につきましては、電気通信国家試験センターの「お問い合わせ」に確認し了承頂いております。
出典:一般財団法人データ通信協会電気通信国家試験センター_電気通信主任技術者_試験問題・解答
[過去問]令和1年第2回問5(3)
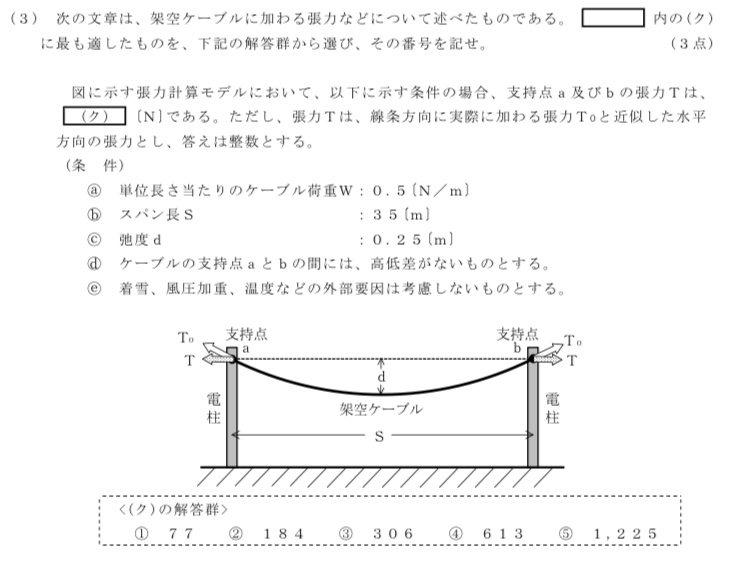
[解説]
「弛度と張力の公式②」を用いて簡単に解くことができます。
=612.5 / 2
=306.25
答えは「整数とする」となっているので、小数点以下を切り捨てし、
A.306
③が答えになります。
[過去問]平成31年第1回問5(5)
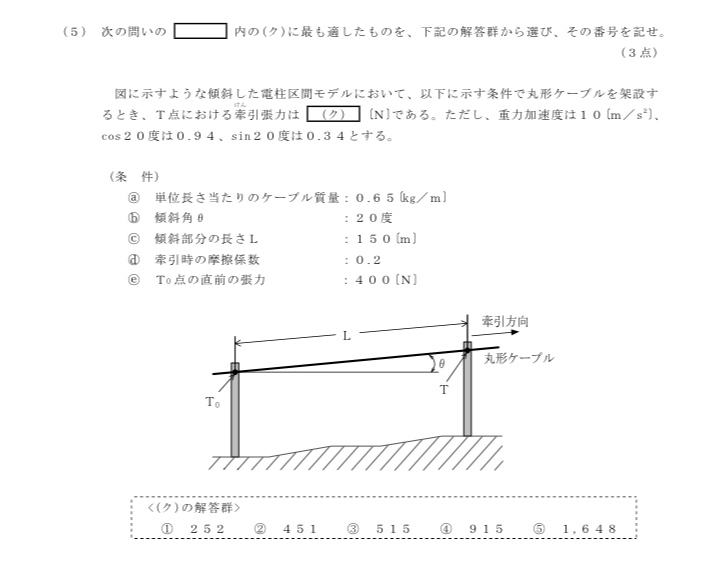
[解説]
「直線区間の牽引張力の公式」を用いるのですが、少し応用問題となります。
ここで、問題文にcos・sinと記載があるので、三角関数を使用することが想像できます。問題は傾斜した区間での牽引張力ですので、x軸方向とy軸方向に力が働きますので、
=400+(0.2×10×0.65×150×0.94)
+(10×0.65×150×0.34)
=400+183.3+331.5
=914.8
答えは「最も適したもの」とあるので、
A.915
④が答えになります。
[過去問]平成30年第2回問5(5)

[解説]
「直線区間・屈曲部直後の牽引張力の公式」を用いて解くことができます。
問題文に「交角20度」とありますが、cos・ sinの数値が記載されていないことから無視して良いと言えます。
直線区間 Txy=100+(0.5×10×0.5×200)
=100+500=600
【Y点での屈曲部直後の張力】
屈曲部直後 Ty=Txy・K
=600×1.2=720
【Y-Z間の牽引張力】
直線区間 Tyz=Ty+(0.5×10×0.5×100)
=720+250=970
よって、Z地点での牽引張力は、
A.970
④が答えとなります。
「牽引張力の公式」より張力増加率は
K=e(μθ)乗
[※θの単位はrad]
の数式で求めることができ、この数式に今回の問の摩擦係数と角度を当てはめると、[※20度≒0.35rad]
K=e(0.5×0.35)乗=e(0.175)乗
≒1.1912≒1.2
問題文で与えられている通り、張力増加率は「1.2」になります。
[過去問]平成30年第1回問5(5)
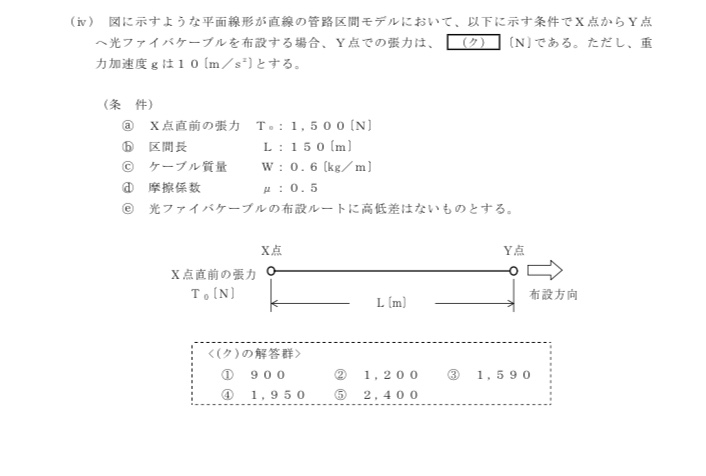
[解説]
「直線区間の牽引張力の公式」を用いて簡単に解くことができます。
直線区間 Txy=1500+(0.5×10×0.6×150)
=1500+450=1950
よって、Y点での張力は
A.1950
答えは④になります。
後書き
上記の問題同様に、出題されるパターンは決まっているので、
公式とパターンを覚えると確実に解くことができます。
電気通信主任技術者(線路)を受験しようと考えている方は参考にしてみて下さい。