電気通信主任技術者(線路)の専門科目である「通信線路」の問1に頻出されている【一様線路の一次定数及び二次定数と減衰量の関係】についてポイントを解説していきます。
近年で2-3回に1問は出題されていますので、この計算問題を確実に解けるようにして8点を確保しましょう!
牽引張力の問題同様、数式とパターンを覚えるだけで解けますので、参考にしてみて下さい。

電気的定数が一様に分布している一様線路において、電気特性は「分布定数回路」として扱うことができ、一次定数と二次定数は下記のように与えられる。
L:インダクタンス
G:往復導体の単位長当たりの漏れコンダクタンス
C:静電容量
β:「位相定数」
γ:「伝搬定数」
Zo:特性インピーダンス
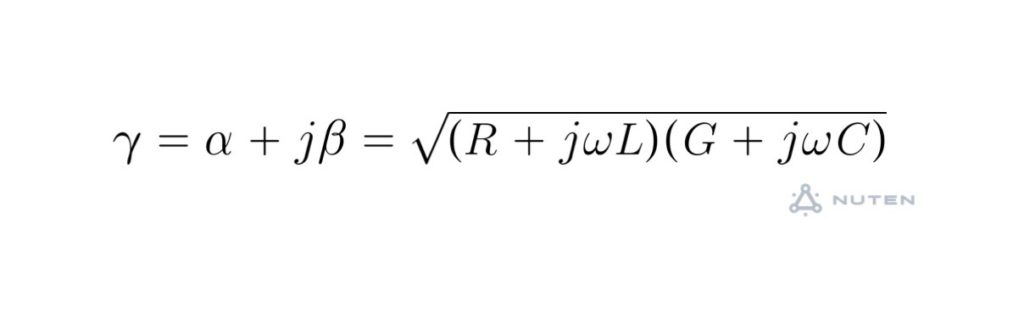
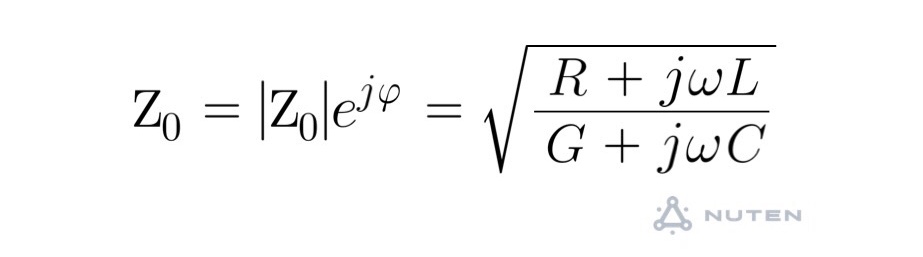
ω:伝送波の角速度
ψ:特性インピーダンスの偏角
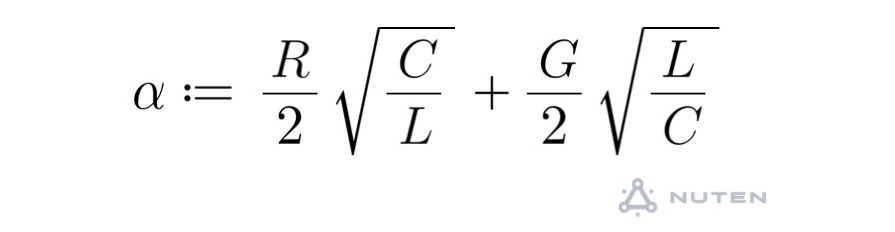
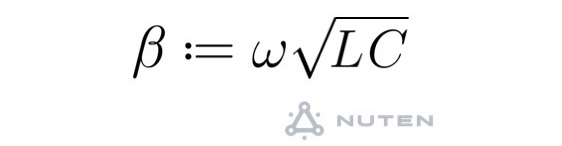
ここで、Rは表皮効果や「近接効果」などにより、「周波数の平方根」に比例して大きくなり、αも同様に大きくなる。
さらに、この線路の減衰量が最小となるR、L、G、Cの関係は「RC=GL」であり、これは、減衰量最小の条件といわれる。
減衰量最小条件は、無ひずみ伝送が成立する条件でもあり、伝送に用いる周波数帯域が全体にわたり、「特性インピーダンス」が一定であること、減衰定数αが一定であること及び「位相定数」が周波数に比例することが必要である。
※音声周波数程度の低周波の場合、一般に、一次定数間においての「 LG≪RC 」関係が成立するため、角周波数をωとすると二次定数のα及びβは、次式で近似できる。
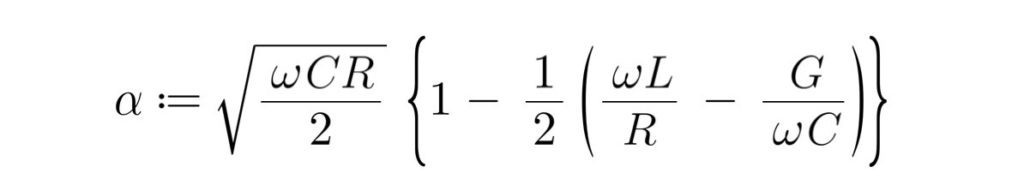
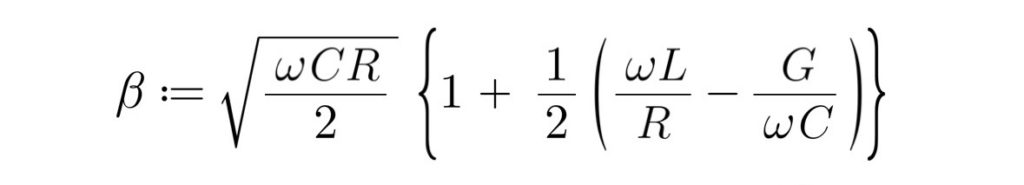

2年分(年2回の4試験分)の過去問利用につきましては、電気通信国家試験センターの「お問い合わせ」に確認し了承頂いております。
伝搬定数と特性インピーダンス
令和1年第2回の問1(1)

平成30年第2回の問1(1)
この問題は
平成24年第1回の問1(1)
にも同様に出題されています。

平成30年第1回の問1(1)

平成29年第2回の問1(1)
この問題は
平成24年第2回の問1(1)
にも同様に出題されています。

平成26年第2回の問1(1)

後書き
一様線路の問題は、毎回同じパターンで出題されていますので、上記ポイントと過去問を抑えていれば確実に解くことができます。
電気通信主任技術者(線路)を受験しようと考えている方は、参考にしてみて下さい。